CS3452 Theory of Computation Important Questions

CS3452 Theory of Computation

Important Questions

Unit 1 Part B

1. Prove that the statement “if n ≥ 5, then n can be written as a sum of 2’s and 3’s” by inductive principle.
2. Construct a DFA that accepts the string over an alphabet (0,1}, number of O’s is multiples of 3.
3. Prove that the language L is accepted by NFA with 6-transition, then there exist DFA also accept the same language L. 
   

   

4. Construct a DFA for the following Language and check whether w=^ prime 1101′ is a valid string or NOT.
   L(G)=\ w| w \in (0, 1) and w starts with 0 and has odd length or it starts with 1 and has even length).
5. Explain the DFA minimization algorithm with an example.
6. Construct NFA accepting the set of strings Sigma = \{0, 1\} such that two O’s are separated by a string whose length is 4i, for some i >= 0
7. Prove that for every L recognized by an NFA, there exists an equivalent DFA accepting the same language L.

Unit 2 Part B

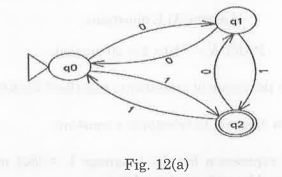
1. From Fig. 12(a), find the regular expression for the following DFA. 
   

   

2. Construct an NFA for the regular expression (01+10)* 10*.
3. Show that the language L = {0*12 | n > 0} is not regular.
4. Prove if L and M are regular language, then so is L-M.
5. Prove that the set of regular languages is closed under complementation. (i.e., If L a regular language then L’ is also a regular language). Give an example.
6. How to determine in two Regular Expressions are equivalent or NOT? Are (a*) and (c + aa*) equivalent wrt. ∑ = {a,b}?
7. Prove that regular expressions are closed under union, concatenation, Kleene closure, complement.
8. Prove that any language accepted by a DFA can be represented by a regular expression and also construct a finite automata for the regular expression 10+(0+11)0*1.

Unit 3 Part B

1. Construct a PDA that accept the L = abcd / n, m ≥ 1) by empty stack.
2. Prove that if PDA P is constructed from CFG G, then L(P) L(G).
3. Grammar G / S →S1S|0 Is this grammar G is ambiguous? Justify.
4. Construct a CFG for the language given below.
   L(G) = {w\we (a,b) and w is an odd length palindrome). Also check whether w ‘babab’ is a valid string or not.
5. Construct an empty store Push Down Automata (PDA) for the below mentioned language:
   L(G) = {wiwe (a,b)} and w is of the form a”b” and n≥1). Also mention the state transitions of this PDA while parsing the string w = ‘aaabbb’.
6. Design a PDA that will accepts strings (a+b)* in which the number of a’s is greater than the number of b’s given the alphabet Σ={a,b}.
7. Convert the above PDA to its equivalent CFG.

Unit 4 Part B

1. Prove that L=\ a ^ n | n is perfect square) is not context free.
2. Design a Turing Machine to compute
   f(m, n) = m – n, ifm >= n
   = 0 , if m < n
3. Explain the programming techniques for Turing Machine
4. Demonstrate the working model of to perform proper subtraction.
5. Construct a Turing machine to accept the following language.
   L(G) = {w/we (0,1) and wis of the form 0″1″ where n≥1}
6. Convert the following grammar to CNF (7)
   S → ASB |ε             A→aAS |a
   B→SbS| A|bb
7. Design a Turing machine to compute proper subtraction.

Unit 5 Part B

1. Show that 3-CNF SAT is NP complete.
2. Find the following languages are recursively enumerable.
   (i) Union of recursively enumerable languages.
   (ii) L and complement of L are recursively enumerable.
3. Give short notes on Recursive and Recursive Enumerable languages.
4. Explain the philosophy behind Travelling salesman problem (TSP). Analyze the computational complexity for the same. Show how the decision version of the TSP belongs to the class of NP-Complete problem.
5. Prove that Post Correspondence Problem is undecidable.
6. Write short notes on P and NP completeness.
7. Explain about Universal Turing Machine.
8. Discuss Travelling Salesman Problem in terms of P and NP completeness.