CS3401 Algorithms Important Questions

CS3401 Algorithms Important Questions

Unit 1

1. Explain in detail about various asymptotic notations and it’s properties.
2. Use substitution method to show that T(n)=2T(n/2)+n is O(nlog(n)).
3. With a suitable example, illustrate the time and space complexity analysis of binary search and linear search.
4. Explain the working of naïve string matching algorithm with ABCCDDAEFG as the text input and CDD as the search string.
5. Write the asymptotic notations used for best case, average case and worst case analysis of algorithms. Also write an algorithm of finding maximum element of an array and perform best, worst and average case complexity with appropriate order notations.
6. Write and explain naïve string mating algorithm.
7. Suppose T=1011101110 and p=111. Find all valid ships.
8. Write an algorithm to perform linear search on an array of ‘N’ numbers. Illustrate the best case, average case and worst case complexity of the linear search algorithm with an example.
9. What is pattern searching? Outline the steps in the Rabin-Karp algorithm for pattern searching with an example.

Unit 2

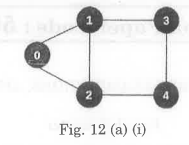
1. Write the pseudocode for BFS and DFS traversals on the graph given below in fig. 12 (a) (i) and compare the time and space complexity of the two traversals. 
   

   

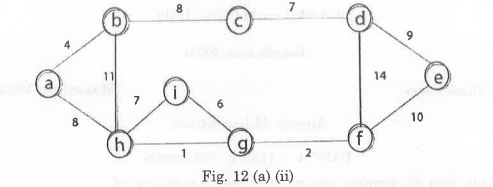
2. Find the Minimum Spanning Tree of the following graph in fig. 12 (a) (ii) using Kruskal’s algorithm.  
   

   

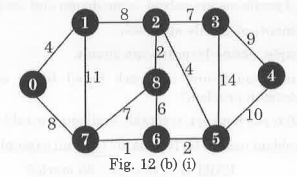
3. Given a graph and a source vertex in the graph, find the shortest paths from the source vertex 0 to all vertices in the given graph 12 (b) (i). 
   

   

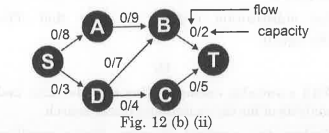
4. Using Ford-Fulkerson algorithm find the maximum possible flow in (5) the network given below Fig 12 (b) (ii).
   

   

5. Write and explain the pseudo code for breadth first search and discuss its time complexity.
6. Write and explain the pseudo code for Floyd Warshall algorithm and write its time complexity.
7.  Outline the breadth first search graph traversal algorithm and depth first search graph traversal algorithm with an example.
8.  Explain the Dijkstra’s shortest path algorithm with an example.

Unit 3

1.  Demonstrate divide and conquer approach by Performing quick sort on the following values. 44, 33, 11, 55, 77, 90, 40, 60, 99, 22, 88
2. Using Dynamic programming, Solve matrix chain multiplication problem.
3. Solve the following problem using Greedy algorithm. Given activities with their start and finish times, select the maximum number of activities that can be performed by a single person, assuming that a person can only work on a single activity at a time.
4. Explain in detail about merge sort. Illustrate the algorithm with a numeric example and provide complete analysis of merge sort algorithm.
5. Explain the dynamic programming approach of matrix multiplication with an example.
6.  Outline the merge sort algorithm with an example.
7. What is a Huffman tree? Outline the steps to build a Huffman tree using greedy algorithm design paradigm with an example.

Unit 4

1. Explain the steps in solving n-queens problem using backtracking approach.
2. Solve the following subset sum problem using back tracking. Let S (3,7,9,13,26,41); d(sum)=51.
3. Discuss briefly about the general method of branch and Bound approach and state how it differs from backtracking.
4. Write down the steps to solve subset sum problem using backtracking approach explain with an example.
5. Write down the steps to solve Travelling Salesperson problem using branch and bound approach. Explain with an example.
6. State the Hamiltonian circuit problem. Outline the steps to find the Hamiltonian circuit using backtracking algorithm design paradigm with an example.
7. State the Knapsack problem. Outline how Knapsack problem can be solved using branch and bound algorithm design paradigm with an example.

Unit 5

1. Show that if an algorithm makes atmost a constant number of calls to polynomial time subroutines and performs an additional amount of work that also takes polynomial time, then it runs in polynomial time.
2. Show that the satisfiability of Boolean formulas in 3-conjunctive normal form (3- CNF) is NP-complete.
3. Illustrate polynomial-time approximation scheme for the sum of subsets problem.
4.  Illustrate the working of Miller-Rabin randomized primality test.
5.  Write short notes on the following:
   (i) NP algorithms
   (ii) NP Hardness
   (iii) NP-Completeness
6.  Elaborate NP-complete problem and NP-hard problem with an example.
7. Outline the randomized quick sort algorithm with an example.